豪爾赫·路易斯·博爾赫斯的小說《小徑分岔的花園》描述了一個迷宮,這個迷宮極其複雜,沒有人可以走出來。故事的講述者說到他知道道路的方向,然後就開始跑題了:
指示說一直向左拐,這讓我想起,走迷宮的一般方法就是如此,用這種方法可以發現一個確定的迷宮的中心點。我對迷宮有研究。我是彭睢的曾孫,這可非同尋常。彭睢曾經管轄雲南省,後來辭職,專心寫一部小說,這部小說本可能比《紅樓夢》更著名。同時他還在建造一座迷宮,任何進入迷宮的人都會迷路。他花了13年時間做這兩件沒什麼關聯的事,直到一個陌生人把他謀殺了。他的小說看起來語無倫次,他的迷宮也消失了。我在英國的樹下思索著關於這座消失的迷宮的一切:我想像這座迷宮是至高無上的完美巔峰;我想像它消失在稻田下或水底;我想像它是無限的,不是由八角形的亭子和往復的路徑構成,而是由河流、省份和王國構成……我構想的是迷宮的迷宮,一個錯綜複雜的迷宮,它涵蓋過去和未來,並且以某種方式把星辰包括進去。
「迷宮」這個詞起源甚早,而且含義不固定。在古希臘羅馬時期,迷宮是一種建築,至少有一部分建在地下,故意設計得令人暈頭轉向。希羅多德(Herodotus)認為,鱷城附近的埃及迷宮(建成於公元前1795年)是一個比金字塔還偉大的奇觀。這座迷宮包括3 000個房間,其中一半建在地上、一半建在地下,迷宮裡的柱子像森林一樣茂密,一直延伸到人們視力所及的範圍之外。希羅多德遊歷了地上的一半迷宮,但是未被獲准觀賞地下部分。他被告知,神鱷在地下守護著法老的墓穴。許多古代作家記錄了這座迷宮的逐漸衰落,它的遺址始終沒有消失。1888年人們發掘了它的地基,面積是800 000平方英尺(800×1 000)。
在西方文化中,最著名的迷宮是古希臘克里特島上的彌諾陶迷宮。在希臘神話中,彌諾陶是一頭牛首人身的怪獸,居住在一個巨大的迷宮中央,這座迷宮是代達羅斯為克里特國王邁諾斯設計的。在克里特打敗雅典之後,邁諾斯國王下令,雅典人每9年向彌諾陶進貢7名童男和7名童女作為祭品。這些進入彌諾陶迷宮的人無一生還。雅典王子特修斯自願作為祭品進入迷宮。邁諾斯的女兒阿里阿德涅告訴特修斯,進入迷宮時沿路拉開絲線,這樣就能找到出路。特修斯用這個辦法殺死了彌諾陶,終止了進貢。
這個神話故事也許是根據雅典進貢者的傳說演化而來的。在克里特人的制海權處於巔峰時,雅典派人向克里特進貢。也許他們在克里特見到了一些他們不理解的東西(莫非是一個戴著牛頭面具的神秘教派的祭司?),而後他們的故事逐漸變味兒了。我們不知道古代克里特的迷宮是什麼樣的,我們甚至不知道它是否真的存在。在克里特語中,「迷宮」可以指迷宮一樣的建築,巖洞或者曲折的山洞(克里特地形以巖洞為特色),或者在推理中導致的不可解的困境——即悖論。在克里特文明衰落以後,克諾索斯宮殿遺址被稱為「迷宮」,也許只是為了諷刺性地把它比作巖洞。殘存的克諾索斯錢幣顯示,他們有一個建造迷宮的規劃,它似乎是一個人工建造的迷宮,不僅僅是天然的巖洞。20世紀初,考古學家在克諾索斯發現了宮殿殘骸,但是沒有發現什麼與迷宮相似的地方。
另一個隱藏在傳說中的迷宮是羅莎蒙德的閨房(Rosamond Bower)。據推測,它建於12世紀的英國伍德斯托克(Woodstock)的一個公園裡。國王亨利二世把自己的情婦羅莎蒙德夫人(Rosamond the Fair,約1140~約1176年)藏匿於這個非常玄妙的迷宮中,以免妻子阿基坦的埃莉諾(Eleanor of Aquitaine)發現。亨利二世利用一個秘密的「竅門」找到正確的路線,到達幽會地點。根據傳說,埃莉諾也找到了一個「竅門」:她沿著一根絲線追蹤,也到達了迷宮的中心,令羅莎蒙德飲鴆自盡。這個故事是編造的,在14世紀以前尚未出現。羅莎蒙德的閨房是否真的存在,以現代的眼光看它是否稱得上迷宮,這些問題都很難說。不那麼浪漫的歷史學家猜測,它不過是一座設計簡陋的房子,外面有一些迷惑人的通道。
現代迷宮差不多都是花園迷宮,通道兩側用角樹(在英國常見)或紫杉製成籬笆封死。都鐸王朝時期和斯圖亞特王朝時期,花園迷宮在英國很興盛。迷宮的設計者通常留出一條有記號的秘密路線通向出口,這是走迷宮的竅門。知道這個竅門,就可以毫無困難地找到出路,出入自如。
迷宮留下許多奧妙。走迷宮問題屬於NP完全問題。它是一類普遍性的問題中的一個,有可能難倒最強大的計算機。
NP完全
世界就是一個由縱橫交錯的關聯和關係組成的迷宮。「NP完全」(NP-Complete)這個名稱客觀而準確地表達了這種狀態。從字面上看,「NP完全」是「非確定性多項式時間完全」(nondeterministic polynomial-time-complete)的縮寫。這個令人望而生畏的術語定義了一個基本而普遍的問題種類,在哲學思辨和實際應用兩方面都有重大意義。
NP完全問題是30年來始終困擾著計算機程序員的一類問題。計算機自問世以來,其運算速度越來越快,功能越來越強大。20世紀80年代末的計算機的運算速度大約比50年代末的計算機快3萬倍。有一個炫耀的說法:「如果汽車技術的發展與計算機技術保持相同的速度,那麼相當於一輛勞斯萊斯汽車應當以超音速行駛,而價格低於1美元。」然而,在20世紀60年代中期,計算機科學家開始意識到有些事不對勁。有些普通問題極難用計算機解決(也很難用已知的方法處理)。採用更強大的處理器或者投入存儲空間更大的內存也無法產生可以期望的差別。這些問題逐漸被稱為「難以處理的」或「內在困難的」。
「旅行推銷員」問題即為一例。許多古老的謎題書都介紹過這個問題。這是一道數學題:一個推銷員必須到達幾個城市,城市之間的距離已知,要求你為一個推銷員設計一條最短路線。這個問題擊敗了最強大的計算機。關鍵在於組合數學,一個本身不太大的集合產生了數量巨大的組合。解決這個問題的已知的最好辦法並不比比較每一條可能路線的總英里數高明多少。隨著城市數的增加,計算量如雨後春筍般激增,很快就突破了任何可以設想的計算機的計算能力。
NP完全作為一類問題首次在1972年的一篇論文中得到清晰的表述,論文的作者是加州大學伯克利分校的理查德·卡普。從此以後,NP完全在幾十個意外的領域受到關注。小孩的謎語、謎題、遊戲和腦筋急轉彎中有許多NP完全問題的例子。如果找到了可高效解決NP完全問題的「解法」,那將是價值連城的發現(不過大多數計算機科學家認為不大可能找得到)。美國、蘇聯以及其他技術發達國家的軍事安全在這個時代以NP完全為基礎[1],而這個基礎並不牢靠,在信息時代,再沒有什麼比這更令人如芒在背了。超級大國的敏感數據是用「公開密鑰」密碼保護的,這種密碼以大型的、實際不可解的NP完全問題為基礎。類似的密碼為商業私人數據和政府數據庫提供安全保障。許多種類各異的問題實際上是相互等同的,這個發現在哲學上也是發人深省的。毫無疑問,「很少有技術術語像『NP完全』這樣快速地聲名遠播」——麥克爾·R·加裡(Michael R.Garey)和大衛·S·約翰遜(David S. Johnson)影響廣泛的著作《計算機與難以駕馭性:NP完全理論導論》(1979)就以這句話開篇。
「NP完全」是一個非常難以理解的抽像說法。我們最好用具體的例子解釋一下。迷宮不僅可以用來比喻我們對知識的探求,在方法論上,迷宮還等價於我們的邏輯方法(從一個適當的、抽像的視角看)。迷宮預示了演繹方法中的核心問題——悖論發現問題。
迷宮算法
我們以這個問題開始對NP完全的探討:是否存在解迷宮的一般方法?
是的。事實上,存在好幾種方法。並非所有的迷宮都需要動腦筋。單行線迷宮從頭到尾都只有一條通道,沒有岔道,沒法走錯。許多中世紀的迷宮迂迴曲折但是沒有岔道,唯一的通道會通向一棵樹或一座神殿。早期的英國教堂墓地設計成這種類型的迷宮,象徵迂迴曲折的人生道路——虔信者在世間邪惡的誘惑下穿行。
克諾索斯的彌諾陶迷宮可能就是沒有歧路的。錢幣的圖案顯示了一條沒有岔道的通道。如果你在這樣一座迷宮裡遭遇彌諾陶,你只需做一件事:掉過頭跑。這樣你永遠都不會走進死胡同,另外,也許這些錢幣只是表明一種設計風格,而非一張真正的地圖。還有一種可能:這些圖案也許展示了在更複雜的通道網絡中應當怎麼走。除非有岔道,否則你用不著拿一根絲線標記路線。
每座迷宮至少有一個入口,而且大多數迷宮都有一個終點——在迷宮中你試圖到達的一個地點。終點通常在迷宮的中心附近,當然,終點也有可能只是迷宮邊界上的一個出口。[2]破解迷宮的目的是找到一條路線,從入口走到終點。路線也許只有一條,也許有多條。當連接入口和終點的路線不止一條時,一個潛在的謎題是發現最短路線。
有些迷宮的入口不止一條。這與僅有唯一入口的迷宮並無本質不同。你的第一個選擇是從哪個入口進入,這個選擇是在進入迷宮以前做出的,但是這與在迷宮內選擇路徑沒什麼兩樣。有些迷宮有多個終點,要求遊客走遍迷宮的各個部分,或者一系列由雕像、長椅或其他東西標示出來的地點中的每一個。路易十四在凡爾賽建造了一個著名迷宮,遊客需要找到39座根據伊索寓言設計的雕塑。每座雕塑的原型都是伊索寓言中會說話的動物,水柱從它們的嘴裡噴出來,形成噴泉。最後,還有一類迷宮是沒有終點的,這種迷宮的走法就是進去閒逛,然後找條路出來。
在迷宮格局中,每個分岔處稱為一個「節點」。節點是通道交叉的地方,在節點處你必須做出選擇。入口、終點和死胡同的終端也被視為節點。兩個節點之間的通道被稱為一個「枝」。任何迷宮都可以用簡化的圖來表示,在圖中,「節點」用點表示,「枝」用線表示,點和點之間用線連接。用數學術語來說,迷宮是一張「圖」。
幾乎所有物理形式的迷宮都是二維的。這意味著,枝和枝之間從不交叉。在三維迷宮中可以有天橋和地道,枝和枝可以交疊,如同高速公路的立交橋。
在圖上解迷宮和實際走迷宮不是一回事。面對謎題書上印出來的迷宮地圖,通常只利用眼睛就可以解決,人眼會自動地把迷宮當作一個「完形」。但是當你身處於一個實際的迷宮內部時,通道兩側被籬笆或石頭封閉,你很難在頭腦中形成一個整體圖像。高明的設計者會把某些節點設計得非常相似,讓你覺得自己在同一條路上兜圈子,而實際上你到達的是一個新地點。此外,在圖上解迷宮可以用一些由來已久的方法,例如,把終點當作起點進行倒推(這種方法有時使問題簡化,有時則更麻煩),或者勾掉所有死胡同,從而使路線變得更清晰。但是在實際的迷宮內部,這些法子都用不上。
迷宮的難度與各節點處發出的「枝」的數量息息相關。如果每個節點處都只有一個枝,那麼這個迷宮一定是單行線迷宮。我們可以把節點想像成兩顆珠子,在珠子之間有一條線,無論這條線如何盤旋環繞,一個不變的事實是,它總是連在兩顆珠子之間。沙特爾教堂的迷宮就是單行線迷宮,這個迷宮沒有牆,是用藍色和白色的大理石在地板上鋪出來的。
如果每個節點處有兩個枝,迷宮同樣毫無難度可言。我們可以把它設想成一堆珠子串在一條線上。走這樣一個迷宮時,你不用做出選擇。實際上,你通常不會把連接兩個枝的連接點視為一個節點。把這兩個枝看作連續的一個枝更簡單,所謂的節點不過是在這個枝上打了一個結。
在迷宮裡,一個真正的岔道至少需要幾條通道匯聚在一個點(三條路形成三岔路口)。節點處匯聚的枝越多,迷宮就越難走。
大多數近年來的迷宮按照習慣採用了接近直線的設計,道路和限制通道的籬笆構成密密麻麻的蜂巢,填滿整個區域。這使得此類迷宮比每個節點發出四個枝還要難。凡爾賽迷宮採用了更靈活的設計。各個枝不必要地平行,許多枝匯聚在一個單獨的節點上。最高紀錄是一個節點上匯聚了5個枝。凡爾賽迷宮的設計師安德烈·勒諾特雷(Andre Le Notre)在尚蒂伊建造了另一個迷宮,其中心節點匯聚了8個枝。
下表介紹了關於幾個著名迷宮的統計數據。有幾處,節點和枝的數目應當如何計算有待商榷。在每個場合,細心的遊客需要做出決定的地點都被我算作一個節點,入口、終點和死胡同的終端也被當作節點,但是只有兩個枝的冗余節點被排除在外。最後一列是平均每個節點匯聚的枝的個數,這個數量大致反映了迷宮的難度。
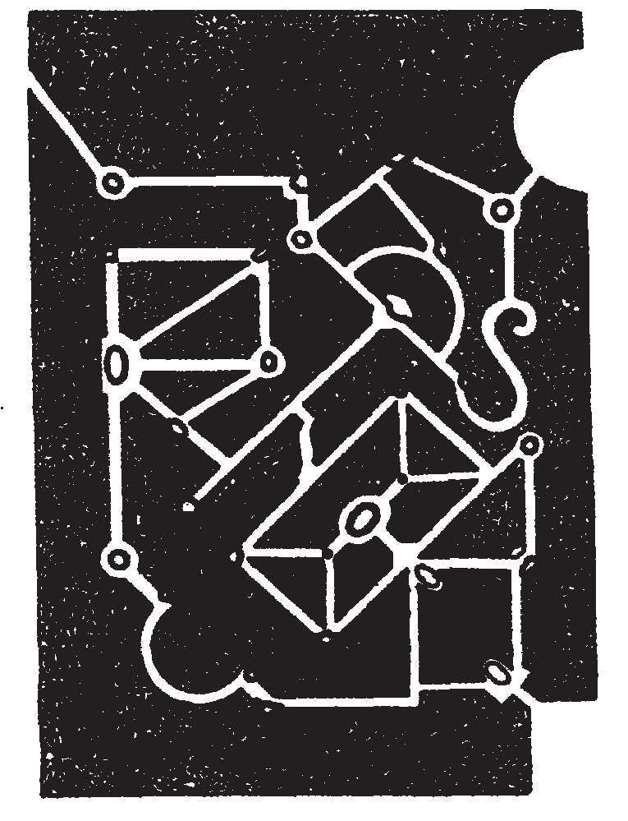
凡爾賽迷宮
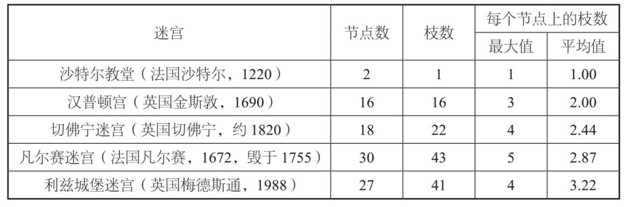
右手法則
最著名的迷宮算法是「右手法則」:每當你面臨選擇時,選最右面的枝。如果走到了一個死胡同,折回來退到上一個節點,選擇你沒走過的枝中最右面的一條。為了具體地應用這條法則,最好的辦法是始終用右手摸著右側的籬笆,絕不漏掉右側的枝。
當然,右手本身沒什麼特別之處。採用「左手法則」一樣行得通。唯一需要注意的是,一旦進入迷宮,就必須堅持同一條法則。
為什麼這條法則行得通?它不是一個單純的習俗。「按順時針方向擰緊螺絲」是一個單純的習俗,但是你完全可以製造一枚螺紋方向相反的螺絲。右手法則比簡單的習俗更深刻,它依賴於迷宮的拓撲結構。
我們來研究一張畫在紙上的迷宮的規劃圖。被籬笆封鎖的區域塗成綠色,綠色區域之間的白色部分是迷宮中可以通行的部分。在許多迷宮中,被籬笆封鎖的區域連成一片。此時實際上只有一道籬笆,儘管它可能是蜿蜒曲折的。這個迷宮看起來像一個形狀詭異的國家。對比地圖上的國家,代表國土的綠色區域被邊界線包圍。邊界線是一條單獨的封閉曲線(邊界線對應迷宮的籬笆)。這條曲線的任何一個部分與任何一個其他部分是連在一起的。因而,走迷宮的時候,只要把右手放在籬笆上耐心地往前走,一定會經過迷宮的所有部分。
前文提到童子軍迷路算法——沿著溪流可以找到有人煙的地方,實際上,右手法則的基本原理與此類似。整個北美是一塊大陸,北美的海岸線(包括江河構成的凹陷)是一條封閉曲線。沿著河岸或者海岸線走,最終一定會到達新奧爾良(也可以到達任何一個位於河流或海岸線上的地點)。在迷宮中,也許會包含被籬笆分隔開的「島嶼」,但是,只要入口處的籬笆和終點處的籬笆屬於同一個島嶼,右手法則就可以生效。
右手法則(或者左手法則)的優點是簡單。它的缺點有兩個:首先,效率不高。跟隨這條法則你會走遍右側(或左側)的每一條死胡同。在大多數場合,存在一條通向終點的短得多的路線。其次,右手法則並非在所有迷宮中都能生效,這一點更為糟糕。顯然,所有已知的、在19世紀20年代以前建造的迷宮用這條法則都能走通。此後,數學家斯坦諾普伯爵設計了一個更複雜的迷宮,它坐落在肯特郡的切佛寧。
切佛寧迷宮有八個被籬笆分隔開的「島嶼」,因而右手法則不再有效。入口和終點不在同一個島嶼上。如果你依照右手法則走這座迷宮,你會圍著一個區域兜圈子,永遠無法到達終點。(就好比在長島沿著河岸和海岸線走,永遠無法到達新奧爾良一樣。)這類迷宮需要一個更複雜的算法。
特雷莫算法
所有更強大的迷宮解法都需要某種方法以確保人們不是在兜圈子。你需要在路上做標記,沿路放絲線、撒麵包屑、折彎樹枝,如此等等。否則,你必須有極好的記憶力,能記住籬笆的形狀,並且保證自己能認出所有曾經走過的地點。
有一種名為「特雷莫算法」的通用方法可以確保解決任何迷宮問題。根據法國數學家愛德華·盧卡斯(Edouard Lucas)的《娛樂數學》(1882)一書的記載,這種方法是特雷莫(M.tremaux)發明的,因而命名為特雷莫算法。這種方法可以說是前文提到的特修斯沿路放絲線的方法的精細化算法。
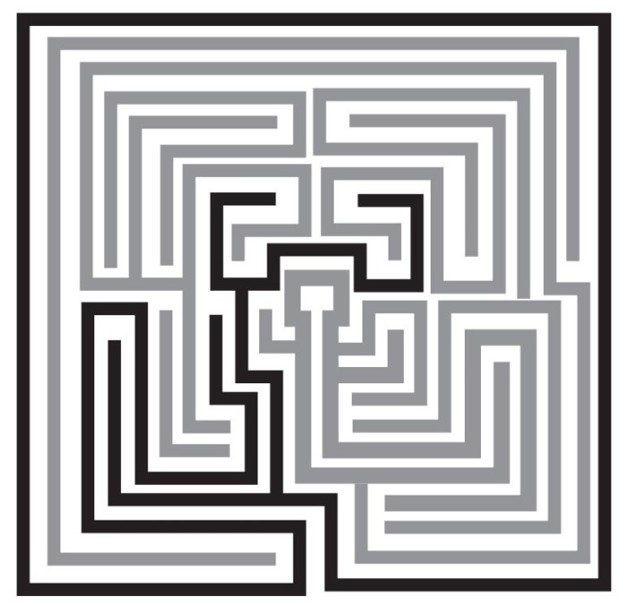
切佛寧迷宮(籬笆圍成的外部「島嶼」以黑色表示)
特修斯沿路放絲線保證自己可以原路返回入口處,不至於迷路。但是絲線不能幫助特修斯找到彌諾陶的窩。特修斯可能會走到某個岔路口,發現自己在兜圈子。當他決定下一步選哪一條路時,他可以利用這個信息加以改進,這種想法是合理的。特雷莫算法就是這麼做的。
走進迷宮後,首先隨便選一條路,沿路做記號,可以利用絲線或任何手邊的東西(下文的敘述中採用麵包屑)一直走,直到達到目標(如果走運的話),或者走進一條死胡同,或者迷宮中的一個你以前來過的岔路口(證據是你留下的記號)。
一旦走進一條死胡同,就退到上一個節點。(你別無選擇!)記住在回來的路上也要做記號。如果你曾經在一條死胡同裡一進一出,路上將留下兩行麵包屑。這個記號提醒你下次不要再走進去。在特雷莫算法中,任何一條路你都不會走兩次以上。
當你走到迷宮中的一個以前來過的節點時(可能是通過另外一條路來過),進行如下操作:
如果你是從一條新路到達的(也就是說,你的身後只有一行麵包屑),轉身沿原路退回上一個節點。否則:
如果有一條沒走過的路,選擇這一條。否則:
任選一條以前只走過一次的路。
這就是全部需要遵守的規則。根據特雷莫算法,你會在迷宮內完成一次完整的旅行,每一條路你都走過了兩次,兩個方向各一次。當然,在到達終點以後就可以停下了,沒有必要完成整個巡迴。
和右手法則一樣,這種算法的效率極低。當然,你有可能非常走運地從入口直接走到終點,但是可能性更大的是,你走完了迷宮的大部分甚至是全部以後才到達終點。
在什麼時機採用右手法則或者特雷莫算法都不算晚。你可以走進一個迷宮,隨心所欲地走,在迷路以後再採用算法。在任意一個點都可以開始執行算法,把這個點當作另一個「入口」。特雷莫算法將引導你從這個點出發完整地遊歷整個迷宮,包括終點和實際的入口。這兩種算法不僅可以用於花園迷宮,在令人暈頭轉向的建築中也有效。如果你在五角大樓或盧浮宮裡迷路了,你可以利用特雷莫算法走出來。
無限的迷宮
設想一個面積無限延展的迷宮。這個迷宮無邊無際,遍佈整個世界,所以根本沒有入口和邊界。你從迷宮中的任意一個點開始探索,你不知道自己在這個宏大的迷宮中的位置,正如我們不知道自己所處的星系在宇宙中的位置一樣。
這個迷宮的結構非常簡單。在每個節點上,恰好有三個枝交匯。各個節點通過標記相互區分,雕像、長椅、樹木等各種各樣的東西都可以充當標記,你尋找的終點可能就是其中的某一個。
和所有其他迷宮一樣,這個迷宮在本質上也是非理性的。在尋找一個給定的目標的過程中,沒有哪一條路比其他的路更優先,任何一條路都可能是「正確的」。正確與否依賴於這個迷宮是如何建造的。這個迷宮的結構是通過無止無休的自我複製實現的,在複製過程中又加入了變化——意識到這一點令人絕望。假定一個遊客花了若干年探索迷宮中的一個特定區域,到達了已知區域的邊界上的一個岔路口。他面對兩條未探索過的枝,其中一條通向他尋找的標記,但哪一條是呢?實際上,在整個迷宮中他已經探索過的部分一定會多次重複,在某些重複結構中,熟悉的路線連接迷宮的其他部分,因而,右側的路通向終點;但是在其他場合,左側的路才是正確的。當然,這個遊客無法知道他當前的處境屬於哪種情況。對於任何企圖以理性的方法選擇路線的計劃,這都構成了一個嘲諷。
假定你處在這個無限的迷宮中,閒逛了一段時間之後,絕望地發現自己迷路了。你沒有沿路做標記,也不知道自己究竟走了多遠。
在這個困境中,你不想採用特雷莫算法。只要你新走的路沒有和以前走過的路交叉,特雷莫算法就不會對你的行動給予任何指導。你有可能在迷宮中深入若干英里,越陷越深。在一個無限的迷宮中,你甚至有可能從未與自己走過的路交叉,從未見到終點,也從未再次遇到熟悉的地點。
特雷莫算法和右手法則預先假定,即使走遍迷宮的全部或一個很大的部分也沒什麼大不了的,只要確保自己不是在不停地兜圈子,最終到達終點就行。特雷莫算法實際上鼓勵優先探索迷宮中較遠的區域。根據此算法,選擇未走過的枝總是優先於熟悉的枝,而且,除非不得已,你應該盡量避免與自己走過的路交叉。在有限的迷宮中,這些建議是合理的,因為終點幾乎總是距離入口相對較遠。否則的話,迷宮的主人就浪費了自己的地產,付給維護灌木的園丁工資,卻沒有增加迷宮的趣味性,這是沒道理的。
但是在無限的迷宮中,你不能浪費時間在未知的區域漫無目標地閒逛。當你迷失方向、但確知目標比較近(與迷宮的整體大小相比)時,你應當首先探索鄰近的區域,在必要時再向外擴展。耶魯大學的厄於斯泰因·奧爾(Oystein Ore)在1959年介紹的一種算法就是如此。
奧爾算法
為了解釋清楚這種算法,最好假定你從一個節點開始。如果你的出發點不是一個節點,那就走到最近的一個節點處。如果不知道哪個方向可通向最近的節點,隨便選一個方向,走到你遇到的第一個結點。這個點就是你的出發點。
從出發點開始,探索交匯於此的每一個枝。在進入每一個枝的時候,在入口處放一塊鵝卵石。對每一個枝的探索僅限於到達下一個節點,然後在這個枝的終點處放一塊鵝卵石,原路返回出發點。
如果遇到死胡同,你就做一個標記。一旦對一個枝做了死胡同的標記,以後就可以忽略這個枝了。做標記的方法可以是在死胡同的入口處拉一條封鎖線,或者擺上一排鵝卵石。
如果某條路轉了一圈又回到最初的節點,那麼你也要把它標記為死胡同。這種路對你也是無用的。
你的興趣在於確定那些通向有新枝的新節點的枝。在探索的第一個階段結束之後,每一條有可能通向終點的潛在路線都已經做了記號——路的兩端各有一塊鵝卵石,而你重新回到了出發點。
下一步,探索的深度達到兩個節點。沿著每一條非死胡同的枝走到新節點,從這個新節點出發探索每一條由此輻射出去的枝,探索方法照舊。在最初的那個枝的兩端各加一塊鵝卵石(此時,這個枝的兩端各有兩塊鵝卵石),對於新探索的第二級的枝,兩端各放一塊鵝卵石。這個辦法可以防止你找不到返回出發點的路,可返回出發點的路有一個特點:路口處的鵝卵石比其他路口多一塊。和第一階段一樣,對死胡同和兜圈子的路做標記,予以排除。如果一個枝通向以前探索過的節點(這個節點至少有一塊作為記號的鵝卵石),在這個枝的兩端也做標記,予以排除。
探索的第三步,深度達到距出發點三個節點處,在每一個探索過的枝的兩端各加一塊鵝卵石。依照以上規則不斷推進探索步驟,直到發現終點、入口或者其他想找的東西。
奧爾算法可以確定通向終點的最短路線(所謂最短是指枝的數量最少,而非物理距離最短)。當然,你的探索過程不是最簡的。但是,如果最短路線需要經過五個節點,你一定可以在探索的第五個階段發現它,而且可以確保它是最短的。
奧爾算法的效率同樣低得可憐。它不是直接對準正確的路線,而是檢查所有可能的路線。這是必不可少的,因為任何一條路線都可能是正確的。
迷宮的NP完全性
下面考慮一個問題。這個問題也許可以稱為無限迷宮問題。你位於E點(E點代表入口,不過這個點和其他點一樣,淹沒於無邊無際的無限迷宮中),你在尋找G點,這個點代表終點,終點可以是迷宮中的任意點。你不知道G點在哪兒,無法在地圖上對G點定位(根本就沒有地圖)。你確信,如果你走到了終點,便可以認出它來,因為終點處有一個已知的標記。根據以上對迷宮的明確規定提出我們的問題:「連接E點和G點的簡單路線是哪條?」
所謂的「簡單路線」,是指不出現自身交叉的路線。如果路線自身交叉,就是在兜圈子。兜圈子總是不必要的,而簡單路線要求的成本較低。簡單路線可能不止一條。如果存在多條簡單路線,其中最短的一條更受歡迎。但是,對於一條簡單路線是否具備「最短」這個優點,你並不是很在乎。畢竟,探索這個無限迷宮是一個令人恐懼的任務,幾乎任何一條能通向G點的路線都是令人滿意的。
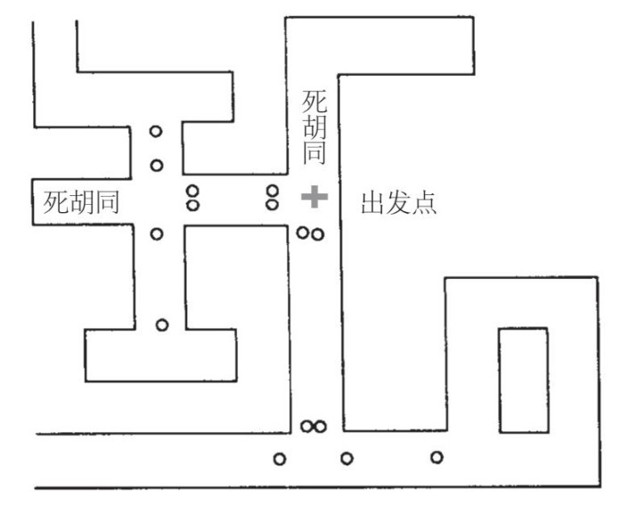
另一個問題與無限迷宮問題密切相關,這個問題可以稱為「迷宮存在性問題」:是否存在從E點通向G點的簡單路線?
我們來看一下為什麼這個問題比較簡單。一旦無限迷宮問題得到了答案(具體指明了一條路線),這個答案本身就回答了存在性問題:簡單路線確實是存在的。即使它無法具體地指明一條路線,在某些情況下,仍有可能表明簡單路線是存在的。我們很自然地認為,一個只需回答「是—否」的問題要比一個也許需要為一個長達數十億個枝的路線不厭其煩地定向的問題簡單。
只有懷疑主義者才會問存在性問題。大多數迷宮探索者有一個基本觀念:所有的點都是以某種方式連在一起的,從此處總可以走到彼處。儘管路線可能曲折而漫長,但是它畢竟是存在的。然而,實情未必如此。有這樣一種可能:迷宮是騙人的,它只有問題卻沒有答案。也許所有道路構成了兩個互相纏繞但彼此分離的網絡,從一個部分無法到達另一個部分。即使假定整個迷宮屬於一個單一網絡,對此我們也永遠無法證明,因為我們的知識僅限於迷宮的局部。在一條具體的路線被發現並得到證實以前,我們總是可以設想通向目的地的路並不存在。
這個「存在性問題」屬於NP完全問題的一種,被稱為「最長路徑」問題。NP完全問題以「困難」著稱,但是這個存在性問題有時不難回答。例如,當G點碰巧距離E點只有一個枝時,隨機的探索幾乎會立刻發現G點,存在性問題和無限迷宮問題同時得到解決。
這很正常。一個一般性問題的特例有可能非常簡單。我們要尋找的是解決存在性問題的成體系的通用方法,這對於最簡單的迷宮和無限的迷宮都有效。
對於一個未知的迷宮而言,不存在快速的解法,事先我們無法知道哪條路更好。我們所能採取的最好的方案就是檢驗幾乎每一條路,直到發現終點。各種各樣的迷宮算法其實只有一個功能:避免不知不覺地兜圈子或者在已知的死胡同和環道上浪費更多的時間。在探索迷宮中的新領域時,算法並不能給你「聰明」的指導。
我們看一下奧爾算法,這個算法的效率和其他算法一樣。你從出發點開始可以發現:這個節點發出了三個枝,每個鄰近的節點同另外兩個節點相連。(在一個鄰近的節點上有三個枝,其中一個枝把這個節點與出發點連在一起,這個枝已經考慮過了。)這六個點中的每一個依次與另外兩個節點相連,這樣新的節點距離出發點又遠了一層。迷宮的節點和枝層出不窮。你探索的枝把你帶到新的節點,而新的節點又產生更多的枝。這些枝中的一部分可能以前探索過(根據以前做的記號可以證明)。在多數場合,需要探索的枝的數量呈指數關係劇烈增長。你對迷宮的瞭解越多,你就越感覺到自己對迷宮的無知。
假定探索一個枝需要1分鐘,奧爾算法的執行過程大致如下:
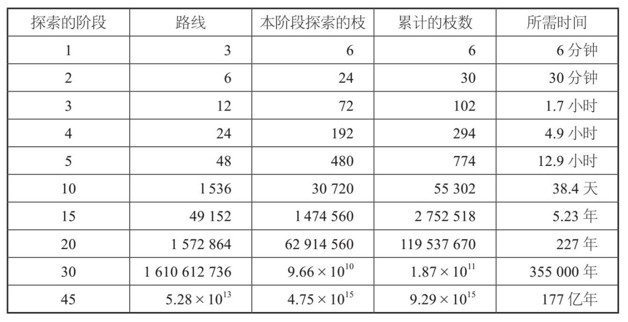
在所有有限的迷宮中,發現新枝的過程最終一定會結束。在某個具體的探索階段過後,大多數新枝會指向已經去過的節點。最終,所有的枝都被走過了,終點一定已經發現。然而,在無限迷宮中,指數增長永不停息。即使終點相對較近,找到終點也會耗費大量的時間,以至於實際上難以找到。也許相距5個節點,需要花費將近一天的時間,但是實際上一旦發現了路線,走到終點只需要5分鐘。搜索一個15個節點遠的終點需要若干年。如果到終點的距離是45個節點,那麼為了找到終點,宇宙的全部時間都不夠用。
我們從計算機程序員的角度來看一下最長路徑問題。你希望用計算機來判定,在一個比較大的迷宮中的兩個點是否被某條路線連在一起。為此,你必須為計算機提供一幅迷宮「地圖」。這幅地圖以表格的形式列出了迷宮中的所有節點和所有的枝。節點標明數字或名字,通過明確一個枝連接哪些節點以及節點之間的距離可以確定枝。(無論採用什麼計數單位,距離都用整數表示。)一個枝可能被表示為「節點16,節點49︰72英尺」。距離是遊客所走的實際長度,而非直線距離。充當入口和終點的節點同樣如此表示。
最長路徑問題還需要考慮一個因素:一個特定的距離n。最長路徑問題問的是,在入口和終點之間是否存在長度大於n的直接路徑。如果你願意,n可以取任意小的值,甚至是0。當n取0時,最長路徑問題轉化為:是否存在一條長度大於0的路徑,這等價於是否存在一條連接入口和終點的任意形態的路徑。
既然存在性問題屬於NP完全問題,比它更難的無限迷宮問題至少和NP完全問題一樣難。如果判定通向G點的路徑是否存在這個問題的難度已經達到了實際不可解的程度,那麼具體指明這樣一條路徑的問題更是如此。
迷宮先知
NP完全問題有一個令人驚異的屬性:其答案很容易驗證。設想你遇到一個先知,無論你問什麼問題,這個先知都能依靠神的啟示立刻給出答案。那些相信先知的全知能力的人帶著問題來問先知,這些問題如此之難,以至於他們解決不了,但是先知卻能立即做出回答。
然而,當先知試圖向所有人證明自己的特異功能時,他遇到了麻煩。他的想法是,通過表明他給出的答案的正確性來證明自己確實是全知的。但有時這是不可能的。
人們問他的問題分兩類。最常見的一類是其他人無法回答的難題:為什麼存在邪惡?神存在嗎?圓周率的十進制小數展開式中小數點後第10100位數字是幾?實際情況是,先知的回答從各個角度來說都是正確而精準的,但是他無法證明這些答案。懷疑者對他冷嘲熱諷:對於這些問題先知可以胡亂給出任意的答案,反正別人也無法揭穿他。即使是相對而言比較現實的問題(例如圓周率的第10100位的數字)也難以驗證,其難度已超出了世界上最強大的計算機的處理能力。
為了證明他的特異功能,這個先知必須回答那些答案可以被檢驗的問題。人們問他的問題中也包括這種,其中某些是懷疑者提出的,提問的目的就是拆穿他。基裡巴斯的首都是哪兒?622 521的平方根是多少?《小婦人》中的姐妹們叫什麼名字?這只密封的箱子裡裝的是什麼?
先知正確地回答了所有這些問題,而且提問者知道先知的答案是正確的。提問者知道這一點,是因為提問者本來就知道答案。問題就出在這兒。這些問題太簡單了,因而不足以確切無疑地證明先知的神力。既然提問者早已通過普通的方法知道了答案,那麼可以設想,先知同樣可以利用普通的方法瞭解或發現。懷疑者會說,他的全知可能是假冒的:他不過是一個計算天才,在一些瑣細的事情方面的知識非常淵博。至於最後一個問題,他採用了「測心術」——表演者在舞台上施展的不入流的騙術。
這兩種結果都是先知的失敗。如果一個問題是其他人無法回答的,懷疑者會指控他捏造;如果一個問題的答案是已知或者可知的,懷疑者會指控他假冒。為了證明自己的全知,先知需要第三類問題,其特點在於:問題很難回答,可一旦說出答案,便很容易驗證。存在這樣的問題嗎?
無限迷宮問題就滿足這個要求。讓懷疑者在這個迷宮中選兩個隨機點,然後讓先知在兩點間確定一條路線。任何人都能輕而易舉地驗證答案正確與否,他們需要做的不過是沿著指定的路線走,驗證一下自己是否到達正確的地點。
這個問題不會是另一個「簡單」的問題嗎?我們必須確保選定的這兩個點足夠遠,沒有人知道連接這兩個點的路線,甚至沒有人可以用正常方法找到一條這樣的路線。算法(包括奧爾算法)的相對低效性保證了這樣一對點的普遍存在。如果兩個點相距20個節點,用普通方法找到一條路線需要若干個世紀。[3]另外,這個問題不會是另一個「困難」的問題嗎?不會,因為我們只需20分鐘就可以檢驗先知的答案(假定每分鐘走過一個枝)。迷宮的一個解比迷宮本身容易太多了。
就本質而言,第三類問題與複雜性理論中的「NP類」很接近。
P和NP
一個一般性的問題不同於一個問題的若干例子。拼版遊戲是一類一般性的問題;把1 500塊碎片拼起來,復原成一幅荷蘭風車的圖案。這是拼版遊戲的一個例子。
NP完全理論判斷問題的難度不是以某些特定的例子為依據,而是以難度隨問題的規模增長而增長的函數關係為依據。在拼版遊戲中,問題的規模反映為碎片的數量。碎片越多,問題越難。問題的難度最好用解題所需的時間衡量。當然,所需時間依賴於你的工作效率,但是這段時間顯然與你為了完成工作而必須比照、處理的碎片數目有非常大的關係。
拼版遊戲有一些非常困難的例子,例如有一種比較新穎的玩法,所有的碎片都是一種顏色。在這種情況下,你必須隨機地比較碎片,判斷它們是否吻合。在這個過程的早期,你需要把每一個碎片和許許多多的碎片比較,這個階段會令你精疲力竭。比較和匹配操作的總體步驟與碎片數量的平方成正比。因此,所需的時間可以表示為包含n2的多項式函數,其中n為碎片的數量。
比較而言,這個問題所需的時間還不算多。在迷宮中,用奧爾算法找到終點所需的時間更接近於2n,其中n是起點和終點之間的節點數。當n較小時,n2和2n之間差別不算巨大;隨著n值的增加,多項式函數和指數函數之間出現一條巨大的鴻溝。你可以解決一個有5 000個碎片的拼版問題,但是你無法解決一個需要5 000次正確選擇的迷宮問題,除非迷宮明顯非常簡單。
從複雜性理論的角度看,所謂「容易」的問題是那些可以在多項式時間內解決的一般性問題。這些問題屬於P類(P代表多項式)。我們把P設想為某處的一個遼闊的國家,粗略地畫在地圖上,但是邊界是清楚的。地圖上的任何一點或者屬於P,或者不屬於P。當然,我們的地圖不大可靠,有時候無法判斷屬於與否。拼版問題是一個屬於P類的點,簡單的算術問題也屬於此類。
另一類問題稱為「NP」,包括所有那些答案可以比較容易地被檢驗的問題(可以在多項式時間內驗證)。如果一個問題是簡單的,那麼答案也是容易檢驗的。如果別無檢驗的辦法,你可以把問題重解一遍,比較一下兩次的答案是否一樣,這樣就完成了檢驗。因此,所有簡單問題(P類)屬於答案容易檢驗的問題(NP)。NP還包括許多P以外的問題,迷宮就是一個例子。這樣看來,NP像是一個更大的國家,而P是NP內部的一個省。如果畫成地圖,大致如下圖。外面的矩形代表所有可能的問題。NP類並不包含所有的問題。有些極端困難的問題,甚至檢驗其答案都是很難的。矩形中NP的圓圈以外的部分代表這類問題。
我們在這個背景下討論先知的問題。第一類問題是困難的,檢驗也是不容易的,它們相當於NP的圓圈以外的問題。第二類問題對應於P類。第三類問題難以回答但容易檢驗,對應於在NP範圍內但不屬於P的問題。
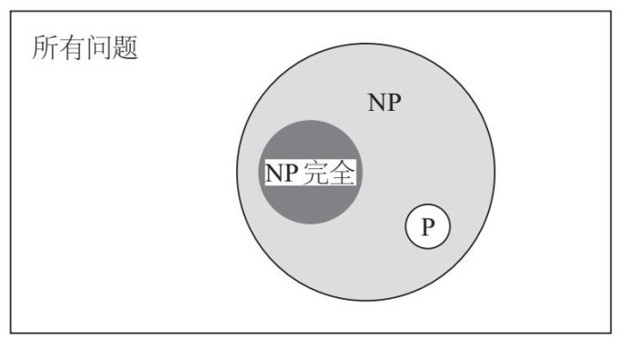
「NP」這個術語(「非確定性多項式時間」)涉及一種被稱為「非確定性計算機」的東西。這種理想化的計算機會特別地被稱為「圖靈機」,這是計算機先驅艾倫·圖靈(Alan turing)構想出來的。非確定性計算機與字面意思不大一樣。從字面上看,它的意思似乎是計算機隨機工作,或是遵循某種不大確切的「算法」(或者一台有自由意志的計算機)。
我們可以這樣設想一台非確定性計算機的操作:我們的計算機不止一台,我們有很多台計算機,計算機的數量有可能是無窮多的。每一台計算機被分配了某個問題的一個可能解,以負責檢驗這個解。
例如,我們的問題是,要在迷宮中找一條路線,全體計算機(在這個例子中是機器人)從入口處出發。每當這支機器人搜索隊走到迷宮的一個岔路口時,他們兵分數路,每條路分配一隊人馬。搜索隊在每個新的岔路口不停地分派人馬,直到把所有可能路線探索完畢。
至少有一個機器人實際上從入口走到了終點。現在我們集中考慮這個機器人。它用了多長時間?很可能沒用多少時間。迷宮的解通常較短,迷宮的難度在於嘗試所有錯誤的路徑以及退回到出發點的過程。一台非確定性計算機用來「解」一個問題所需的時間就是用來檢驗一個猜出來的解的時間。
NP問題大致相當於科學探索所面對的問題。當科學家試圖建立新的真理時,他的地位很像上文提到的先知。科學最關心的假說與NP問題的答案類似:這些假說可以非常容易地被證實或反駁。
在NP問題和科學之間還有更驚人的聯繫——邏輯演繹本身就是一個NP問題。
最難的問題
在NP類問題中,哪個問題最難?1971年,斯蒂芬·庫克證明,「可滿足性」和NP中的任何一個問題相比至少同樣難。他的證明顯示,在NP中不存在更難的問題,因為所有NP問題都可以轉化為可滿足性問題。
隨之而來的是理查德·卡普的發現(1972):許多不同種類的難題都屬於可滿足性問題。這些形態各異的問題來自圖論、邏輯學、數學遊戲、數論、密碼學、計算機編程等領域,它們都和可滿足性問題同樣難。由最難的NP問題構成的類稱為「NP完全」。用維恩圖(Venn Diagram)表示,NP完全在NP的圓圈內,但位於P外。
嚴格地說,NP完全是一個不穩定的區域,也許並不真正存在。我們尚未證明NP完全問題無法在多項式時間內解決。我們的證據僅僅是經驗性的:理論家和計算機程序員傾注多年的心血,試圖在多項式時間內解決NP問題,但是毫無例外地失敗了。在實際中,一旦證明一個問題屬於NP完全,則可以認為有充分理由證明,這個問題不存在高效率的解決方法。
我們還可以勉強設想,存在一種尚未發現的超級算法,可以在多項式時間內解決所有的NP問題。如果確實有這種算法,那麼P、NP和NP完全就全變成一回事兒了,我們可以把它們合在一起表示為一個圓圈。
如果存在一種高效率的解法——一個神奇的竅門,那麼我們從邏輯前提中可以推出的東西 (像福爾摩斯那樣)實際上就沒有任何限制。反過來說,如果可滿足性問題和NP完全問題沒有高效率的解法,在現實中就一定存在大量的永遠不會被發現的真理。我們強烈地感到,這樣一種解法是不存在的。所有人都像華生醫生那樣,錯過了大量可見的線索。
這意味著,對於哪些邏輯問題是可解決的,存在著一個關於其規模的相對嚴格的限制。在迷宮問題中,一旦迷宮規模超過一定限度,就變成實際不可解的了;同樣的道理,一旦一個邏輯問題超過一定的複雜程度,也會變成實際不可解的。一個明顯的推論是,我們關於實在世界的推理也是有限度的。
經驗目錄
悖論意義重大、影響深遠,超過了其表面看起來的程度。如果某人相信一些自相矛盾的觀念,那麼這些觀點中至少有一些是他沒有理由相信的。因而,理解一組觀點(至少)意味著有能力發現觀念中的矛盾。所以說,發現悖論的問題——即可滿足性問題——是知識的界標。在試圖全面理解某事的含義的過程中,已經內在地包含可滿足性的難度。
在奠定牛頓的萬有引力理論基礎的因素中沒有一樣是古希臘人不知道的。疾病的細菌理論原本有可能提前幾個世紀提出和確立——如果某人發現了正確的聯繫。同理,此刻一定也有我們尚未完成的綜合,雖然所需的材料已經擺在面前。非常可能的是,解決「如何預防癌症」、「第10顆行星在哪兒」這些問題所需的全部事實已然齊備,但是還沒有人發現組織這些事實的正確秩序。不僅如此,也許我們正在錯過關於這個世界的各種各樣的邏輯結論。這些結論有可能隱藏在我們見到、聽到的每件事裡,但是其複雜性有一點點超出了我們的理解力。
愛因斯坦寫道:「全部科學的宏大目標是,從最小數量的假說或公理出發推導出最大數量的經驗事實。」[4]把人類的全部經驗加在一起,包括從冰川紀至今所有人曾經看到、摸到、聽到、嘗到或聞到的一切。從理論上說,這些信息可以彙集為一個巨大的目錄,這個目錄是一個簡單的列表,對經驗不做任何解釋。對夢境、幻象、胡思亂想和錯覺詳盡描述,與「真實」的經驗並列。二者中哪個是真實經驗(如果有的話),留給目錄的讀者自己確定。
這個目錄必然包含作為自然科學的基礎的全部觀察。對鳥、星星、蕨類植物、水晶和草履蟲的全部觀察都可以在目錄中找到。這個目錄也包含所有曾做過的科學實驗中的那些哪怕最微小的細節。目錄中還包括,在1887年那個特殊的日子,邁克爾遜和莫雷對下午稍晚時候的陽光照耀在儀器的鏡子上的印象。[5]牛頓曾見過的所有蘋果的顏色、尺寸、形狀、運動速度以及加速度等信息也被搜集在目錄中。
科學不是簡單的經驗目錄。首先,任何人的大腦都無法容納全部人類經驗的整體。目錄必須包括你經歷過的一切,這就會佔據迄今為止你的整個生命中的全部注意力!科學對人類經驗(或經驗的某些方面)進行壓縮,達到一個可處理的形式。我們真正感興趣的是理解目錄所描述的這個世界。總的說來是這樣,雖然某些特殊場合併非如此。在科學哲學中有一個惱人的問題:這種過程可能進行到何種程度?
每一個經驗對未知的世界的某些部分的真值都做出了限制——和在邏輯謎題中一樣。當然,未知事物間的關係可能非常微妙,每一個事物都必須用一系列的「如果」來限定。也許你的一個經驗是:你聽到你的朋友弗雷德說,他上個星期二見到了尼斯湖怪獸。經驗的實際輸入也許是這樣:
如果弗雷德沒犯錯,他也沒有撒謊,並且外部世界不是幻象,那麼在星期二尼斯湖怪獸存在。
這些「如果」從句是必不可少的輔助性假設,它們使證實複雜化。
把經驗目錄輸入一台超級計算機,編好程序,讓它進行推演。這個任務只需要邏輯,而邏輯正是計算機的強項。在這個任務完成以後,計算機甚至可以把推演結果按重要性排序,重要的衡量標準是一個結果可以解釋多少不同的經驗。推演結果列表的第一條應當是人類可以知道的最重要的事實。
雖然以上介紹只是幻想,但是它確實展現了科學哲學中某些最核心的問題的基本框架。連鎖推理是科學的基礎,它的一致性可以在多項式時間內識別和檢驗。這些簡單的邏輯問題相當於單行線迷宮(在每個節點處只有一或兩條枝的迷宮),簡單得不值一提,並且與「正常」的迷宮(每個節點處有三條或更多的枝)不同。更複雜的推演包括含有三或四個未知量的前提,解這類問題需要指數時間(實際上是無法完成的)。也許有一大類可以解釋我們的感覺經驗的邏輯推演是我們永遠無法發現的。
把我們的經驗設想為迷宮,把關於經驗的邏輯真理設想為遍佈迷宮的路徑。可滿足性問題的NP完全性表明,我們永遠無法窮盡所有的潛在路線。
和宇宙一樣大的計算機
計算機科學家拉裡·J·斯托克邁耶(Larry J. Stockmeyer)和阿爾伯特·r·邁耶(Albert R. Meyer)設想了一台大小和宇宙一樣的計算機,以此來形象地展示處理NP問題的極高難度。他們表明,我們在想回答許多關於宇宙的問題時,會發現宇宙並不夠大。
假定我們試圖把所有已接受的觀念列成一個清單。就像笛卡兒一樣,我們希望從一片空白開始,並且非常小心地把觀念填進去。在任何一個觀念被填進去之前,首先再次檢查已經被列進清單的觀念,以確保增加的新觀念與已有的觀念不產生矛盾。這個檢驗即為可滿足性問題。
也許你會認為,為此只需要把清單瀏覽一遍,確保準備加入的新觀念不與任何一個以前列入的觀念直接矛盾。然而,實際情況沒有這麼簡單。
顯然,新的觀念有可能與舊的觀念矛盾。如果新的觀念是「所有烏鴉都是黑色的」,而舊觀念中有一條「所有烏鴉都不是黑色的」,在這裡你就遇到了矛盾。[6]最危險的是這種情況:三個或更多命題,各自獨立地看都是可以成立的,但是合在一起構成矛盾。通常,「悖論」這個術語專門指這種情況,矛盾不是一目瞭然的。
假定新的觀念是「所有草都是綠色的」,清單中可能已經包含了兩個語句:
所有乾草都是黃色的。
乾草是草。
這兩個語句若加上新語句就產生了矛盾。如果你僅僅一對一對地檢查——在三個語句中拿出兩個來檢查是否相互一致,你就會遺漏這個矛盾。為了排除這種情況,有必要在清單中一對一對地取出所有可能的命題組合,一一檢驗它們加入新命題後是否一致。這極大地增加了檢查的工作量。但是這還不算完。也許還有更精緻的悖論,只在四個、五個或更多命題合在一起考慮時才顯現出來。在100萬個觀念中加入一個觀念,即使在原來的觀念中任意取出999 999個觀念與新觀念合在一起都是一致的,整體上還是有可能出現矛盾。
需要檢查的事實太多了,顯然必須借助於計算機。我們從l號觀念開始(這個觀念也許是「我思故我在」)。為了讓計算機能夠處理,這個觀念被表示為關於布爾未知量的一個邏輯命題,下一步,我們準備加入一個新的觀念,2號觀念。我們指示計算機對照1號觀念進行檢查,看看是否出現矛盾。此時,只需一次邏輯檢驗(比照2號觀念和1號觀念)。
現在,清單中有兩個觀念,我們準備加入第三個。此時必須進行三次檢驗:與1號觀念比照;與2號觀念比照;與1號、2號合在一起比照。
第四個觀念必須和7個命題集合進行比照:分別與1、2、3號比照;分別與1和2、1和3、2和3比照;與l、2、3合在一起比照。
事實上,一個新的觀念必須與當前清單上的所有可能子集合在一起檢驗。n件東西的子集數計算公式是一個指數函數:2n。這個公式把空集也計算在內,其實我們不必考慮空集。非空子集的數量是2n–1。
假定這些觀念(或其中的某些信息)在邏輯上足夠複雜,因而無法避免指數時間的算法。此時,需要進行比較的次數如下表:
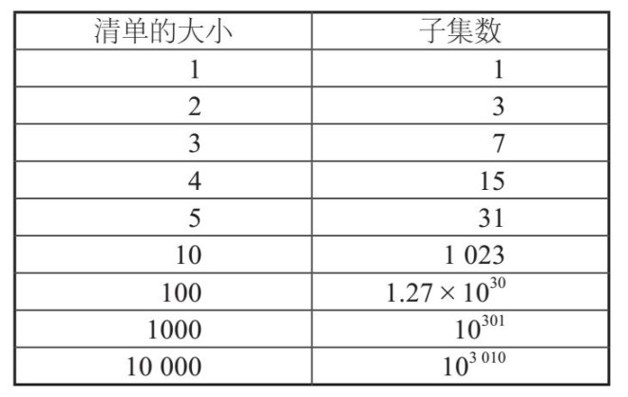
即使這個清單的規模非常有限,比方說,只包含100個觀念,它的子集數也是一個天文數字。為了接受第101個觀念,它必須與這個清單包含的1030個子集對比檢驗。
怎麼會這樣呢?你可以寫下第101個觀念,然後很快地確信其中並無悖論,這不是很明顯的嗎?
確實如此。你可以隨機從一部百科全書中抄下100個命題,確保每個命題都提到一些別的命題沒說的東西。但是,我們現在研究的是更一般的情況,清單中的觀念可能有許多是關於同一個未知量的,而且邏輯關係是複雜的。這些觀念有可能互相糾葛,就像卡洛爾豬排問題的前提那樣。這樣我們就必需求助於一種算法——一種很慢的算法。
計算機向清單中加入觀念的過程可以快到什麼程度?
斯托克邁耶和邁耶在分析時,假定有一台「理想」計算機依靠指數時間算法確定某些數學命題的真假。就本質而言,這個分析對可滿足性問題同樣有效。斯托克邁耶和邁耶認為,任何一台計算機的計算能力最終取決於它所包含的元件的數量。在計算機體積一定的條件下,元件越小,處理能力越強。
在最早的數字計算機中,邏輯門採用真空管,而連接採用導線。後來,真空管讓位於晶體管。現在,強大的處理器封裝在一個芯片內。大多數連接是通過印製電路實現的,它們由很薄的金屬膜構成。
沒有人確切地知道,處理器和邏輯門可以小到什麼程度。在實驗條件下,邏輯門可以採用只有幾個原子厚度那麼厚的膜。在這個領域,許多前途遠大的技術尚待開發。斯托克邁耶和邁耶在他們的思想實驗中採用了非常樂觀的假定。他們設想,計算機元件以某種方式可能達到質子的大小。現在我們認為,在可測量的範圍內,質子和中子是最小的。在這台理想計算機中,無論元件多麼小,其直徑不能小於10–15米(負的指數表示分數,這個數是1除以1015,即一毫米的一萬億分之一)。
假定這些質子大小的元件可以像沙丁魚罐頭那樣密密麻麻地塞滿在一個體積給定的物體內,它們可以填充多少個直徑為10–15米的理想球體,就可以填充同樣數量的元件。如果計算機的大小與普通的個人電腦相仿(體積大約為1/10立方米),則大約包含1044個不同的元件。一個體積為一立方米的小型機將包含1045個元件。
在計算機技術中,另一個頭等重要的因素是速度。一個元件需要花費的時間(例如一個邏輯門從一個狀態轉換到另一個狀態的時間)構成瓶頸,任何形式的信息最快只能以光速傳播。因此,一個元件轉換狀態的時間不能超過光通過它所需的時間,否則就意味著,元件的一端以超過相對論所允許的速度「得知」另一端發生的情況。
光穿過一粒質子的直徑所需的時間是3×10–24秒。在斯托克邁耶和邁耶的分析中,理想計算機的元件轉換狀態所需的時間採用這個值。
在現實中,計算機的速度還依賴於元件之間的連接方式以及為處理問題配置的可用資源的完善程度。大多數現在的計算機是串行的,也就是說,在某一個時刻計算機只處理一件事。在任意一個瞬間,計算機處於算法中的一個點。就潛力而言,並行計算機的速度快得多。並行計算機有很多處理器,總任務被分解為子任務,交給各個處理器。在大多數時間裡,並行計算機能夠同時做許多事。
我們不妨奢侈一些,假定這台理想計算機按超精密的並行結構設計。每一個質子大小的元件是一個單獨的處理器。各個處理器用某種類似於連接機器的方式連接起來,以確保相對直接的連接——即使處理器的個數是天文數字。
這台計算機向各個處理器分派子任務,每一個處理器分配到當前觀念清單的一個不同的子集。每個處理器有能力瞬間完成新觀念與當前的子集的比較。在一次轉換狀態的時間內,處理器可以確定是否出現矛盾,然後轉而處理下一個子集,這個時間是3×10–24秒(為了計算方便,把這個數近似設為10–23)。因此,每個處理器在一秒鐘內可以進行1023次檢驗。在體積為一立方米的計算機內部,有1045個處理器。這台計算機每秒鐘能處理1068次檢驗。
這個速度很快。面對一個由225個觀念構成的清單,在一秒鐘之內計算機就完成了所有需要進行的比較。
但是此後,進程突然慢下來了。在增加第226個觀念時,花費1秒鐘;檢驗第227個觀念花費2秒鐘;檢驗第232個觀念大約需要1分鐘。計算機的速度一如既往,但是清單中每增加一個觀念,檢驗的工作量增加一倍。檢驗第250個觀念需要一個多月。當清單擴展到300個觀念時,需要的時間是——3 800萬年!
沒關係,這是一個思想實驗,我們擁有世界上的全部時間。據估計宇宙的年齡大約是100億年,折合成秒則在1017和1018之間。增加一或兩個數量級,得到1019,這是對「永恆」的很恰當的估計。當宇宙的年齡達到現在的10倍時,所有恆星都將熄滅,生命很可能已經消亡。[7]因此,1019秒基本上是可以有意義地談論的時間的最大值。如果一台理想計算機有1045個處理器,從時間的起點開始工作,直到時間的終點,它可以進行的檢驗次數是巨大的1019乘以1045的結果,也就是說,它可以把這麼多個子集與新觀念比較。這個數等於1087,足以處理一個由289個觀念構成的清單。
我們需要一個更強大的計算機。一旦元件的最小尺寸已經確定,為了獲得更強大的運算能力,唯有增加體積,把這台計算機擴大到佔據一個房間、一座房屋……一個國家乃至於一個大陸那麼大。但是無論如何擴大,其終極限度都不能超過宇宙的尺寸。
迄今已知的最遙遠的類星體據估計在120億~140億光年以外。如果宇宙是有限的,一個大膽的估計是,其「直徑」為1 000億光年。1光年略少於1013千米,即1016米。因此,宇宙的直徑大約是1027米,其體積大約是1081立方米。
因此,一台大小同宇宙一樣的計算機可以有1045乘以1081個質子尺寸的元件,這個總數是10126。當然,這是白日做夢。關鍵在於:無論科技發達到什麼程度,任何計算機的元件個數不會超過10126。大腦或任何形式的物理實體都不能超過這個限度。這是一個我們必須接受的極限。如果這樣一台計算機從時間的起點開始工作,直到時間的終點,可以執行10126乘以1042次基本運算,即10168。
10168這個數字是你做任何事的次數的絕對極限。最接近超級任務的情況不過如此,因為人們沒有足夠的時間和空間去實現或超過10168次的任何事。不幸的是,運行10168次邏輯檢驗並不能前進很遠。當清單擴展到包含大約558個觀念時,這台計算機就報廢了。
我們最多只能知道558件事嗎?不,當然不是的。我們根據簡單推理、三段論和連鎖推理可以知道很多事情。558這個粗略的限制針對的是在邏輯上足夠複雜、需要用指數時間算法來檢驗的觀念。如果558個觀念像卡洛爾豬排問題那樣「不規則」,那麼這些觀念組成的集合很可能超出了計算機的處理能力——即使計算機和宇宙一樣大。這就是新的悖論不斷湧現的原因。
在邏輯上複雜的觀念既不罕見,也非不自然。就連那些我們認為簡單的觀念(例如「所有烏鴉是黑色的」)實際上也配備了一系列的輔助性假設,可滿足性的難度不僅限於邏輯謎題。
既然我們甚至不能辨別在我們的比較複雜的觀念中是否包含矛盾,我們就沒有完全理解它們。我們當然無法從這些觀念推出所有可以推出的結論。如果你把邏輯推演當作觀察世界的一個視域,那麼這個視域是有限的。連鎖推理是簡單推理構成的鏈條,它構成了這個視域中的基本視線。通過這種視線,我們在黑暗中看得很遠。對於更複雜的推理,我們則非常近視,無法看清所有東西,甚至無法看清所有蘊含在我們的思想實驗中的東西。有些東西就擺在某個地方,但是我們永遠也看不到。
如果說我們過於低能,無法理解那些我們沒看到的東西,這種評價是不公平的。假如我們遇到了全知者(在關於悖論的討論中全知者經常冒出來),全知者可以向我們指明我們沒看到的東西,而我們有能力證明它們是真的。問題的答案是簡單的——在你看到它以後。
這裡的「我們」包括人類、計算機、宇宙生命以及一切物理機制。NP問題對於所有這些「我們」來說都是困難的。斯托克邁耶和邁耶的思想實驗是奧爾貝斯悖論的一個信息時代的翻版。奧爾貝斯的出發點是我們能看見天空中的星星這個事實,而斯托克邁耶和邁耶的出發點是「整個宇宙不是一台計算機」這個事實。這裡的結論是,這個宇宙中沒有人無所不知。
[1] 原著出版時(1987年),蘇聯尚未解體,美蘇兩國軍備競賽正如火如荼地進行。——譯者注
[2] 經作者同意,此處刪掉了一個中國人不易理解的例子。——譯者注
[3] 「沒有人知道連接這兩個點的路線」這個要求是不必要的,出題者可以知道路線。出題者這樣出題:自己在迷宮中隨機地走過50個節點,記住自己走的路,定義他的起點為E點,終點為G點。僅把E和G告訴解題者,讓解題者找到路線。從解題者的角度看,這道題的難度好比大海撈針;但是從出題者的角度看,這就像回家一樣簡單。——譯者注
[4] 原文此處有筆誤。譯文已改。——譯者注
[5] 指著名的邁克爾遜—莫雷實驗,這個實驗證實了愛因斯坦的光速不變理論。——譯者注
[6] 這個例子不恰當。現代邏輯認為,「所有烏鴉都是黑色的」和「所有烏鴉都不是黑色的」並不矛盾,兩個語句可以同時為真。不過,這並不影響作者的分析。——譯者注
[7] 這個預言有一定的問題。宇宙的演化是新生和消亡並存的。不如說「到了那個時候,宇宙可能已經演化成與現在完全不同的形式」更合適一些。當然,這裡所說的合適與否只是就本語句的語意而言,並不影響作者的邏輯結論。——編者注